Rameoids
Rameoids is a spin off of the classic Asteroids game but instead of shooting the asteroids, we simple crash through them to destroy them. This program does not rely on any graphics engine other than one that creates a window and allows individual pixels to be set. In programming this I explored algorithms and techniques involved in the creation of 2D graphics.
The Graphics Engine
This project aims to build its own graphics library/engine. Its build on top of OpenGL and issues quad commands to OpenGL where each quad represents a pixel in the graphics engines view port. Pixels can be scaled up to analyse what exactly happens during the rendering process.
The primary processes of the rendering pipeline for this game are:
- Creation of objects
- Define polygons and vertices
- Triangulate polygons
- Render each frame
- Update the game state
- Transform the vertices
- Fill triangles
- Draw polygon outlines
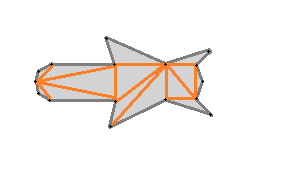
Polygon Triangulation
The program decomposes all polygons into triangles that are then processed separately. Polygon Triangulation for convex polygons this is a very simple process. In this case Fan Triangulation starts at a vertex and splits the polygon into triangle from this point. For concave polygons this is more difficult. This implementation finds two non-consecutive vertices and check if a line connecting them is completely inside the polygon and does not touch any other lines. Once it has found one of these pairs, it splits the polygon along this line into 2 and repeats this recursively until the polygons are reduced to triangles.
Transformations
For each object a transformation matrix is calculated by combining translation, rotation and scaling matrices. Each of the objects vertices is then multiplied by this matrix to obtain the vertex coordinates in final viewport space.
Differential Digital Analyser (DDA)
The DDA algorithm draws lines by calculating the larger of dx and dy and sample along this axis in unit intervals. At each step it calculates the coordinate along the other axis by interpolating its value and then drawing a single pixel at the (x,y) point.
Scan Line Algorithm
Each triangles is filled using the scan line algorithm where by the bounding box of the triangle is found and it iterates left to right, top to bottom. On each pass from left to right, when if first crosses a line of the triangle it enables painting and will draw every pixel it passes until it encounters the next line and painting is toggles off.